For being widely recognized as a “mainstream” automaker, the Lexus LFA supercar is anything but. Its elusive, practically unicorn status, has cemented the car in history as more of an enigma rather than the industry gamechanger...
What is it like to take a seat behind the steering wheel...
A one-of-a-kind 1989 RUF CTR “Yellowbird” Lightweight—nicknamed Redbird—is set to be auctioned...
The Rimac Nevera R has surpassed its predecessor by setting 24 new...
Aston Martin has unveiled the next evolution of its beloved Vantage line:...
Become a member and unlock exclusive access to member-only content, a totally ad-free experience and be part of a vibrant community dedicated to the iconic enthusiast performance cars.
Latest News & Updates
Only the coolest performance, supercar and collector car news
This is the Huayra Codalunga Speedster: an open-air interpretation of the coupé version that won the Design Award at the 2023 Concorso d’Eleganza Villa d’Este. Created by the Pagani Grandi...
Introduced in 2018, Ferrari’s Icona Series pays tribute to the brand’s racing heritage with limited-production models for top clients. The first models, the Monza SP1 and SP2, featured barchetta styling...
Hyper Sportscar Awarded The Rimac Nevera R, which evolves the groundbreaking Nevera from Hyper GT to Hyper Sportscar, has been awarded a coveted Red Dot Award for Product Design 2025....
The Ferrari 812 Competizione A is the open-top counterpart to the stunning 812 Competizione, offering the same extreme performance with the added thrill of open-air driving. As a tribute to...
McLaren Automotive will honour the 2025 Festival of Speed theme, “Champions and Challengers,” by showcasing both its road‑car milestones and racing triumphs. At the heart of “McLaren House” will be...
To commemorate its founding in 1963, Automobili Ferruccio Lamborghini S.p.A. unveiled the Aventador SVJ 63 in both coupe and roadster forms. At its debut, the Aventador SVJ represented the pinnacle...
What happens when you pit Italian turbocharged engineering against German naturally aspirated precision in a drag race? That’s precisely what Carwow set out to discover with the Maserati MC20 and...
Porsche continues to evolve its iconic 911 lineup with the introduction of three new all-wheel drive models for the 2026 model year: the 911 Carrera 4S Coupe, 911 Carrera 4S...
Ferrari has unveiled the Amalfi, a front-mid-engine V8 2+ coupé that replaces the Roma in the Maranello lineup. The Amalfi blends high performance with everyday usability, redefining the modern gran...
Ferrari has unveiled the Amalfi, the long-anticipated successor to the Roma and Top Gear had an early glimpse of it. Named after Italy’s scenic coastal region, the Amalfi is designed...
Features Stories & Member-Only Content
Behind-the-Scenes Coverage, In-Depth Stories and Premium Editorials for Our Members
A true successor to the legendary F1, the 2020 McLaren Speedtail pushes the limits of road car performance with futuristic design and cutting-edge hybrid engineering. Limited to just 106 units...
The Rimac Nevera R is the world’s fastest-accelerating road car. It rockets from 0–60 mph in just 1.8 seconds, hits 125 mph in 4.3, and blasts to 186 mph quicker...
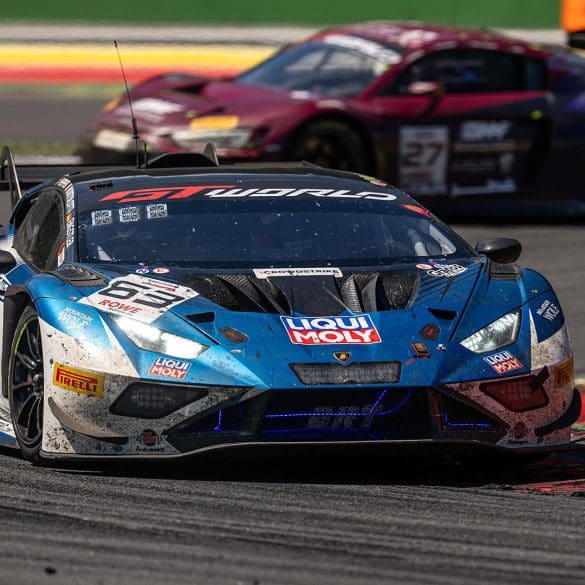
Lamborghini has added a historic milestone to its motorsport legacy by securing its first overall win at the 24 Hours of Spa. Building on previous endurance racing success—including three consecutive...
Nothing less than perfection: that is what is demanded of each example of the Bugatti W16 Mistral¹ before it is delivered to its owner, undergoing an exhaustive and uncompromising quality...
The Koenigsegg Sadair’s Spear is the Swedish hypercar maker’s most extreme track-focused machine yet — and yes, it’s still road-legal. Based on the Jesko, the Sadair’s Spear is lighter, more...
The Hennessey Venom F5 is a hypercar engineered for extreme performance and named after the highest rating on the Fujita tornado scale. Powered by Hennessey’s proprietary 6.6-liter twin-turbocharged V8, nicknamed...
Highlights The hypercar of the 2000s can be seen at the Mercedes-Benz Museum for the first time – as part of the special “Youngtimer” exhibition until 2 November 2025 Developed...
Three years after the original 296 GT3 debuted at Spa-Francorchamps, Ferrari has returned to the iconic Belgian circuit to unveil its next evolution: the 296 GT3 Evo. This isn’t just...
Porsche has once again proven its relentless commitment to pushing the limits of automotive performance, regardless of powertrain. In a remarkable display of engineering versatility, two very different models —...
Lamborghini has been the epitome of incomparable style, outstanding performance, exclusivity and innovation since 1963. Its limited-edition series are the ultimate embodiment of its creative and technical prowess. They are...
The Praga Bohema is a $1.5 million, track-focused hypercar designed to rewrite the rulebook on what a road-legal performance machine can be. The performance figures are impressive—0–62 mph in 3.3...
The CONCEPT AMG GT XX is a pioneering technology program that offers an impressive look into a forthcoming four-door series-production sports car from Mercedes‑AMG. With three axial flux motors and...
Koenigsegg proudly unveils Sadair’s Spear—a track-focused, road-legal masterpiece that redefines performance benchmarks. With more power, less weight, cutting-edge aerodynamics, and bespoke engineering throughout, this limited-edition hypercar pushes the boundaries of...
The Monterey Motorsports Festival is delighted to announce the Peralta S designed by Fabrizio Giugiaro will make its US debut at the show on August 16, 2025. As undoubtedly the...
In this drag race showdown, Mat Watson and his team from carwow will be pitting two hypercars, a Ferrari Daytona SP3, and a Pagani Huayra Roadster BC, to see which...
Our Most Popular Research Hubs
Model Guides, Videos & Cars for Sale. We Have It All If You're a Car Nut