The 2018 Bugatti Chiron you see here is a stunning, two-owner example of the marque’s legendary hypercar, showcasing a truly bespoke specification. Finished in Full Black Exposed Carbon Fiber—a $315,000 option—it is accented with Light Blue...
The Dutch YouTube channel AutoTopNL returns with another high-speed thrill ride—this time...
Ferrari delivered its most expansive and dynamic presence ever at the 2025...
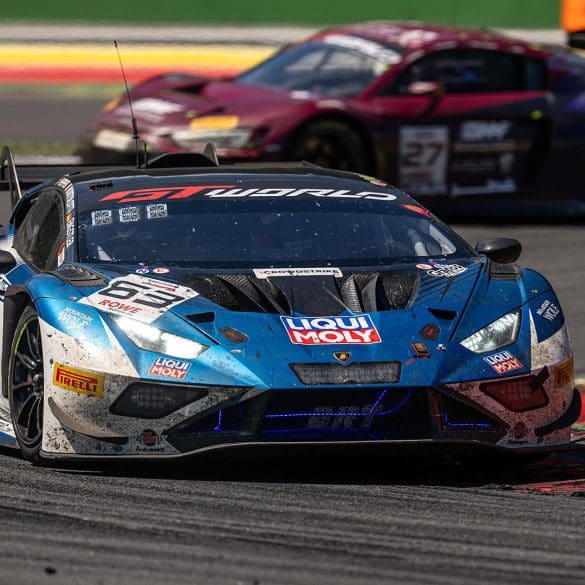
Lamborghini has reaffirmed its commitment to international motorsport and today launches the...
What happens when two of Koenigsegg’s most extreme creations—the Regera and the...
Become a member and unlock exclusive access to member-only content, a totally ad-free experience and be part of a vibrant community dedicated to the iconic enthusiast performance cars.
Latest News & Updates
Only the coolest performance, supercar and collector car news
The Lamborghini Sián FKP 37 represents a pivotal moment in Lamborghini’s history as its first hybrid hypercar. Powered by a 6.5-liter V12 engine paired with a supercapacitor-based 48-volt electric motor,...
For being widely recognized as a “mainstream” automaker, the Lexus LFA supercar is anything but. Its elusive, practically unicorn status, has cemented the car in history as more of an...
What is it like to take a seat behind the steering wheel of the brand new Ferrari F80? Some say it might be the best Ferrari ever made, Ferrari insists...
A one-of-a-kind 1989 RUF CTR “Yellowbird” Lightweight—nicknamed Redbird—is set to be auctioned by RM Sotheby’s at their Monterey event next month with an estimated value between $4.5 and $5 million....
The Rimac Nevera R has surpassed its predecessor by setting 24 new world performance records at the Papenburg test track in Germany, including reclaiming the 0–400–0 km/h (0–249–0 mph) title...
Aston Martin has unveiled the next evolution of its beloved Vantage line: the Vantage S, a nameplate that carries both heritage and high expectations. As the most performance-focused Vantage in...
This is the Huayra Codalunga Speedster: an open-air interpretation of the coupé version that won the Design Award at the 2023 Concorso d’Eleganza Villa d’Este. Created by the Pagani Grandi...
Introduced in 2018, Ferrari’s Icona Series pays tribute to the brand’s racing heritage with limited-production models for top clients. The first models, the Monza SP1 and SP2, featured barchetta styling...
Hyper Sportscar Awarded The Rimac Nevera R, which evolves the groundbreaking Nevera from Hyper GT to Hyper Sportscar, has been awarded a coveted Red Dot Award for Product Design 2025....
The Ferrari 812 Competizione A is the open-top counterpart to the stunning 812 Competizione, offering the same extreme performance with the added thrill of open-air driving. As a tribute to...
Features Stories & Member-Only Content
Behind-the-Scenes Coverage, In-Depth Stories and Premium Editorials for Our Members
McLaren Automotive will honour the 2025 Festival of Speed theme, “Champions and Challengers,” by showcasing both its road‑car milestones and racing triumphs. At the heart of “McLaren House” will be...
To commemorate its founding in 1963, Automobili Ferruccio Lamborghini S.p.A. unveiled the Aventador SVJ 63 in both coupe and roadster forms. At its debut, the Aventador SVJ represented the pinnacle...
What happens when you pit Italian turbocharged engineering against German naturally aspirated precision in a drag race? That’s precisely what Carwow set out to discover with the Maserati MC20 and...
Porsche continues to evolve its iconic 911 lineup with the introduction of three new all-wheel drive models for the 2026 model year: the 911 Carrera 4S Coupe, 911 Carrera 4S...
Ferrari has unveiled the Amalfi, a front-mid-engine V8 2+ coupé that replaces the Roma in the Maranello lineup. The Amalfi blends high performance with everyday usability, redefining the modern gran...
Ferrari has unveiled the Amalfi, the long-anticipated successor to the Roma and Top Gear had an early glimpse of it. Named after Italy’s scenic coastal region, the Amalfi is designed...
A true successor to the legendary F1, the 2020 McLaren Speedtail pushes the limits of road car performance with futuristic design and cutting-edge hybrid engineering. Limited to just 106 units...
The Rimac Nevera R is the world’s fastest-accelerating road car. It rockets from 0–60 mph in just 1.8 seconds, hits 125 mph in 4.3, and blasts to 186 mph quicker...
Lamborghini has added a historic milestone to its motorsport legacy by securing its first overall win at the 24 Hours of Spa. Building on previous endurance racing success—including three consecutive...
Nothing less than perfection: that is what is demanded of each example of the Bugatti W16 Mistral¹ before it is delivered to its owner, undergoing an exhaustive and uncompromising quality...
The Koenigsegg Sadair’s Spear is the Swedish hypercar maker’s most extreme track-focused machine yet — and yes, it’s still road-legal. Based on the Jesko, the Sadair’s Spear is lighter, more...
The Hennessey Venom F5 is a hypercar engineered for extreme performance and named after the highest rating on the Fujita tornado scale. Powered by Hennessey’s proprietary 6.6-liter twin-turbocharged V8, nicknamed...
Highlights The hypercar of the 2000s can be seen at the Mercedes-Benz Museum for the first time – as part of the special “Youngtimer” exhibition until 2 November 2025 Developed...
Three years after the original 296 GT3 debuted at Spa-Francorchamps, Ferrari has returned to the iconic Belgian circuit to unveil its next evolution: the 296 GT3 Evo. This isn’t just...
Porsche has once again proven its relentless commitment to pushing the limits of automotive performance, regardless of powertrain. In a remarkable display of engineering versatility, two very different models —...
Our Most Popular Research Hubs
Model Guides, Videos & Cars for Sale. We Have It All If You're a Car Nut